Lesson 17: Drawing on Canvas

Drawing is deception.

Browsers give us several ways to display graphics. The simplest way is to use styles to position and color regular DOM elements. This can get you quite far, as the game in the previous lesson showed. By adding partially transparent background images to the nodes, we can make them look exactly the way we want. It is even possible to rotate or skew nodes with the transform style.

But we’d be using the DOM for something that it wasn’t originally designed for. Some tasks, such as drawing a line between arbitrary points, are extremely awkward to do with regular HTML elements.

There are two alternatives. The first is DOM-based but utilizes Scalable Vector Graphics (SVG), rather than HTML. Think of SVG as a document-markup dialect that focuses on shapes rather than text. You can embed an SVG document directly in an HTML document or include it with an <img> tag.

The second alternative is called a canvas. A canvas is a single DOM element that encapsulates a picture. It provides a programming interface for drawing shapes onto the space taken up by the node. The main difference between a canvas and an SVG picture is that in SVG the original description of the shapes is preserved so that they can be moved or resized at any time. A canvas, on the other hand, converts the shapes to pixels (colored dots on a raster) as soon as they are drawn and does not remember what these pixels represent. The only way to move a shape on a canvas is to clear the canvas (or the part of the canvas around the shape) and redraw it with the shape in a new position.

SVG

This course will not go into SVG in detail, but we will briefly explain how it works. At the end of the lesson, we’ll come back to the trade-offs that you must consider when deciding which drawing mechanism is appropriate for a given application.

This is an HTML document with a simple SVG picture in it:

The xmlns attribute changes an element (and its children) to a different XML namespace. This namespace, identified by a URL, specifies the dialect that we are currently speaking. The <circle> and <rect> tags, which do not exist in HTML, do have a meaning in SVG—they draw shapes using the style and position specified by their attributes.

These tags create DOM elements, just like HTML tags, that scripts can interact with. For example, this changes the <circle> element to be colored cyan instead:

The canvas element

Canvas graphics can be drawn onto a <canvas> element. You can give such an element width and height attributes to determine its size in pixels.

A new canvas is empty, meaning it is entirely transparent and thus shows up as empty space in the document.

The <canvas> tag is intended to allow different styles of drawing. To get access to an actual drawing interface, we first need to create a context, an object whose methods provide the drawing interface. There are currently two widely supported drawing styles: "2d" for two-dimensional graphics and "webgl" for three-dimensional graphics through the OpenGL interface.

This course won’t discuss WebGL—we’ll stick to two dimensions. But if you are interested in three-dimensional graphics, we do encourage you to look into WebGL. It provides a direct interface to graphics hardware and allows you to render even complicated scenes efficiently, using JavaScript.

You create a context with the getContext method on the <canvas> DOM element.

After creating the context object, the example draws a red rectangle 100 pixels wide and 50 pixels high, with its top-left corner at coordinates (10,10).

Just like in HTML (and SVG), the coordinate system that the canvas uses puts (0,0) at the top-left corner, and the positive y-axis goes down from there. So (10,10) is 10 pixels below and to the right of the top-left corner.

Lines and surfaces

In the canvas interface, a shape can be filled, meaning its area is given a certain color or pattern, or it can be stroked, which means a line is drawn along its edge. The same terminology is used by SVG.

The fillRect method fills a rectangle. It takes first the x- and y-coordinates of the rectangle’s top-left corner, then its width, and then its height. A similar method, strokeRect, draws the outline of a rectangle.

Neither method takes any further parameters. The color of the fill, thickness of the stroke, and so on, are not determined by an argument to the method (as you might reasonably expect) but rather by properties of the context object.

The fillStyle property controls the way shapes are filled. It can be set to a string that specifies a color, using the color notation used by CSS.

The strokeStyle property works similarly but determines the color used for a stroked line. The width of that line is determined by the lineWidth property, which may contain any positive number.

When no width or height attribute is specified, as in the example, a canvas element gets a default width of 300 pixels and height of 150 pixels.

Paths

A path is a sequence of lines. The 2D canvas interface takes a peculiar approach to describing such a path. It is done entirely through side effects. Paths are not values that can be stored and passed around. Instead, if you want to do something with a path, you make a sequence of method calls to describe its shape.

This example creates a path with a number of horizontal line segments and then strokes it using the stroke method. Each segment created with lineTo starts at the path’s current position. That position is usually the end of the last segment, unless moveTo was called. In that case, the next segment would start at the position passed to moveTo.

When filling a path (using the fill method), each shape is filled separately. A path can contain multiple shapes—each moveTo motion starts a new one. But the path needs to be closed (meaning its start and end are in the same position) before it can be filled. If the path is not already closed, a line is added from its end to its start, and the shape enclosed by the completed path is filled.

This example draws a filled triangle. Note that only two of the triangle’s sides are explicitly drawn. The third, from the bottom-right corner back to the top, is implied and wouldn’t be there when you stroke the path.

You could also use the closePath method to explicitly close a path by adding an actual line segment back to the path’s start. This segment is drawn when stroking the path.

Curves

A path may also contain curved lines. These are unfortunately a bit more involved to draw.

The quadraticCurveTo method draws a curve to a given point. To determine the curvature of the line, the method is given a control point as well as a destination point. Imagine this control point as attracting the line, giving it its curve. The line won’t go through the control point, but its direction at the start and end points will be such that a straight line in that direction would point toward the control point. The following example illustrates this:

We draw a quadratic curve from the left to the right, with (60,10) as control point, and then draw two line segments going through that control point and back to the start of the line. The result somewhat resembles a Star Trek insignia. You can see the effect of the control point: the lines leaving the lower corners start off in the direction of the control point and then curve toward their target.

The bezierCurveTo method draws a similar kind of curve. Instead of a single control point, this one has two—one for each of the line’s endpoints. Here is a similar sketch to illustrate the behavior of such a curve:

The two control points specify the direction at both ends of the curve. The farther they are away from their corresponding point, the more the curve will “bulge” in that direction.

Such curves can be hard to work with—it’s not always clear how to find the control points that provide the shape you are looking for. Sometimes you can compute them, and sometimes you’ll just have to find a suitable value by trial and error.

The arc method is a way to draw a line that curves along the edge of a circle. It takes a pair of coordinates for the arc’s center, a radius, and then a start angle and end angle.

Those last two parameters make it possible to draw only part of the circle. The angles are measured in radians, not degrees. This means a full circle has an angle of 2π, or 2 * Math.PI, which is about 6.28. The angle starts counting at the point to the right of the circle’s center and goes clockwise from there. You can use a start of 0 and an end bigger than 2π (say, 7) to draw a full circle.

The resulting picture contains a line from the right of the full circle (first call to arc) to the right of the quarter-circle (second call). Like other path-drawing methods, a line drawn with arc is connected to the previous path segment. You can call moveTo or start a new path to avoid this.

Drawing a pie chart

Imagine you’ve just taken a job at EconomiCorp, Inc., and your first assignment is to draw a pie chart of its customer satisfaction survey results.

The results binding contains an array of objects that represent the survey responses.

To draw a pie chart, we draw a number of pie slices, each made up of an arc and a pair of lines to the center of that arc. We can compute the angle taken up by each arc by dividing a full circle (2π) by the total number of responses and then multiplying that number (the angle per response) by the number of people who picked a given choice.

But a chart that doesn’t tell us what the slices mean isn’t very helpful. We need a way to draw text to the canvas.

Text

A 2D canvas drawing context provides the methods fillText and strokeText. The latter can be useful for outlining letters, but usually fillText is what you need. It will fill the outline of the given text with the current fillStyle.

You can specify the size, style, and font of the text with the font property. This example just gives a font size and family name. It is also possible to add italic or bold to the start of the string to select a style.

The last two arguments to fillText and strokeText provide the position at which the font is drawn. By default, they indicate the position of the start of the text’s alphabetic baseline, which is the line that letters “stand” on, not counting hanging parts in letters such as j or p. You can change the horizontal position by setting the textAlign property to "end" or "center" and the vertical position by setting textBaseline to "top", "middle", or "bottom".

We’ll come back to our pie chart, and the problem of labeling the slices, in the exercises at the end of the lesson.

Images

In computer graphics, a distinction is often made between vector graphics and bitmap graphics. The first is what we have been doing so far in this lesson—specifying a picture by giving a logical description of shapes. Bitmap graphics, on the other hand, don’t specify actual shapes but rather work with pixel data (rasters of colored dots).

The drawImage method allows us to draw pixel data onto a canvas. This pixel data can originate from an <img> element or from another canvas. The following example creates a detached <img> element and loads an image file into it. But it cannot immediately start drawing from this picture because the browser may not have loaded it yet. To deal with this, we register a "load" event handler and do the drawing after the image has loaded.

By default, drawImage will draw the image at its original size. You can also give it two additional arguments to set a different width and height.

When drawImage is given nine arguments, it can be used to draw only a fragment of an image. The second through fifth arguments indicate the rectangle (x, y, width, and height) in the source image that should be copied, and the sixth to ninth arguments give the rectangle (on the canvas) into which it should be copied.

This can be used to pack multiple sprites (image elements) into a single image file and then draw only the part you need. For example, we have this picture containing a game character in multiple poses:

By alternating which pose we draw, we can show an animation that looks like a walking character.

To animate a picture on a canvas, the clearRect method is useful. It resembles fillRect, but instead of coloring the rectangle, it makes it transparent, removing the previously drawn pixels.

We know that each sprite, each subpicture, is 24 pixels wide and 30 pixels high. The following code loads the image and then sets up an interval (repeated timer) to draw the next frame:

The cycle binding tracks our position in the animation. For each frame, it is incremented and then clipped back to the 0 to 7 range by using the remainder operator. This binding is then used to compute the x-coordinate that the sprite for the current pose has in the picture.

Transformation

But what if we want our character to walk to the left instead of to the right? We could draw another set of sprites, of course. But we can also instruct the canvas to draw the picture the other way round.

Calling the scale method will cause anything drawn after it to be scaled. This method takes two parameters, one to set a horizontal scale and one to set a vertical scale.

Scaling will cause everything about the drawn image, including the line width, to be stretched out or squeezed together as specified. Scaling by a negative amount will flip the picture around. The flipping happens around point (0,0), which means it will also flip the direction of the coordinate system. When a horizontal scaling of -1 is applied, a shape drawn at x position 100 will end up at what used to be position -100.

So to turn a picture around, we can’t simply add cx.scale(-1, 1) before the call to drawImage because that would move our picture outside of the canvas, where it won’t be visible. You could adjust the coordinates given to drawImage to compensate for this by drawing the image at x position -50 instead of 0. Another solution, which doesn’t require the code that does the drawing to know about the scale change, is to adjust the axis around which the scaling happens.

There are several other methods besides scale that influence the coordinate system for a canvas. You can rotate subsequently drawn shapes with the rotate method and move them with the translate method. The interesting—and confusing—thing is that these transformations stack, meaning that each one happens relative to the previous transformations.

So if we translate by 10 horizontal pixels twice, everything will be drawn 20 pixels to the right. If we first move the center of the coordinate system to (50,50) and then rotate by 20 degrees (about 0.1π radians), that rotation will happen around point (50,50).

But if we first rotate by 20 degrees and then translate by (50,50), the translation will happen in the rotated coordinate system and thus produce a different orientation. The order in which transformations are applied matters.

To flip a picture around the vertical line at a given x position, we can do the following:

We move the y-axis to where we want our mirror to be, apply the mirroring, and finally move the y-axis back to its proper place in the mirrored universe. The following picture explains why this works:

This shows the coordinate systems before and after mirroring across the central line. The triangles are numbered to illustrate each step. If we draw a triangle at a positive x position, it would, by default, be in the place where triangle 1 is. A call to flipHorizontally first does a translation to the right, which gets us to triangle 2. It then scales, flipping the triangle over to position 3. This is not where it should be, if it were mirrored in the given line. The second translate call fixes this—it “cancels” the initial translation and makes triangle 4 appear exactly where it should.

We can now draw a mirrored character at position (100,0) by flipping the world around the character’s vertical center.

Choosing a graphics interface

So when you need to generate graphics in the browser, you can choose between plain HTML, SVG, and canvas. There is no single best approach that works in all situations. Each option has strengths and weaknesses.

Plain HTML has the advantage of being simple. It also integrates well with text. Both SVG and canvas allow you to draw text, but they won’t help you position that text or wrap it when it takes up more than one line. In an HTML-based picture, it is much easier to include blocks of text.

SVG can be used to produce crisp graphics that look good at any zoom level. Unlike HTML, it is designed for drawing and is thus more suitable for that purpose.

Both SVG and HTML build up a data structure (the DOM) that represents your picture. This makes it possible to modify elements after they are drawn. If you need to repeatedly change a small part of a big picture in response to what the user is doing or as part of an animation, doing it in a canvas can be needlessly expensive. The DOM also allows us to register mouse event handlers on every element in the picture (even on shapes drawn with SVG). You can’t do that with canvas.

But canvas’s pixel-oriented approach can be an advantage when drawing a huge number of tiny elements. The fact that it does not build up a data structure but only repeatedly draws onto the same pixel surface gives canvas a lower cost per shape.

There are also effects, such as rendering a scene one pixel at a time (for example, using a ray tracer) or postprocessing an image with JavaScript (blurring or distorting it), that can be realistically handled only by a pixel-based approach.

In some cases, you may want to combine several of these techniques. For example, you might draw a graph with SVG or canvas but show textual information by positioning an HTML element on top of the picture.

For nondemanding applications, it really doesn’t matter much which interface you choose. The display we built for our game in this lesson could have been implemented using any of these three graphics technologies since it does not need to draw text, handle mouse interaction, or work with an extraordinarily large number of elements.

Summary

In this lesson we discussed techniques for drawing graphics in the browser, focusing on the <canvas> element.

A canvas node represents an area in a document that our program may draw on. This drawing is done through a drawing context object, created with the getContext method.

The 2D drawing interface allows us to fill and stroke various shapes. The context’s fillStyle property determines how shapes are filled. The strokeStyle and lineWidth properties control the way lines are drawn.

Rectangles and pieces of text can be drawn with a single method call. The fillRect and strokeRect methods draw rectangles, and the fillText and strokeText methods draw text. To create custom shapes, we must first build up a path.

Calling beginPath starts a new path. A number of other methods add lines and curves to the current path. For example, lineTo can add a straight line. When a path is finished, it can be filled with the fill method or stroked with the stroke method.

Moving pixels from an image or another canvas onto our canvas is done with the drawImage method. By default, this method draws the whole source image, but by giving it more parameters, you can copy a specific area of the image. We used this for our game by copying individual poses of the game character out of an image that contained many such poses.

Transformations allow you to draw a shape in multiple orientations. A 2D drawing context has a current transformation that can be changed with the translate, scale, and rotate methods. These will affect all subsequent drawing operations. A transformation state can be saved with the save method and restored with the restore method.

When showing an animation on a canvas, the clearRect method can be used to clear part of the canvas before redrawing it.

Exercises

Shapes

Write a program that draws the following shapes on a canvas:

1. A trapezoid (a rectangle that is wider on one side)

2. A red diamond (a rectangle rotated 45 degrees or ¼π radians)

3. A zigzagging line

4. A spiral made up of 100 straight line segments

5. A yellow star

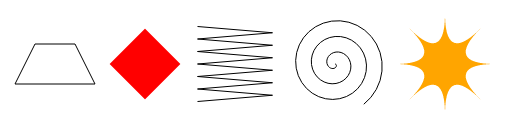
When drawing the last two, you may want to refer to the explanation of Math.cos and Math.sin, which describes how to get coordinates on a circle using these functions.

We recommend creating a function for each shape. Pass the position, and optionally other properties such as the size or the number of points, as parameters. The alternative, which is to hard-code numbers all over your code, tends to make the code needlessly hard to read and modify.

The pie chart

Earlier in the lesson, we saw an example program that drew a pie chart. Modify this program so that the name of each category is shown next to the slice that represents it. Try to find a pleasing-looking way to automatically position this text that would work for other data sets as well. You may assume that categories are big enough to leave ample room for their labels.

You might need Math.sin and Math.cos again, which are described in earlier lessons.

let middleAngle = currentAngle + 0.5 * sliceAngle;
let textX = Math.cos(middleAngle) * 120 + centerX;
let textY = Math.sin(middleAngle) * 120 + centerY;

A bouncing ball

Use the requestAnimationFrame technique that we saw in earlier lessons to draw a box with a bouncing ball in it. The ball moves at a constant speed and bounces off the box’s sides when it hits them.

ExplorableJS is a course by the Learning Technologies Research Group of RWTH Aachen University. It is based on  "Eloquent JavaScript" (3rd Edition, 2018) by Marijn Haverbeke. Content is reused according to CC-BY-NC 3.0. ExplorableJS is licensed as CC-BY-NC 4.0.